Jenis-Jenis Tumbukan (Lenting Sempurna, Sebagian Dan Tidak Sama Sekali) Beserta Pola Soal
Jika ada dua benda yang bertumbukan dan tidak ada gaya luar yang bekerja pada benda-benda, maka berlaku aturan kekekalan momentum. Akan tetapi energi kinetik totalnya biasanya berubah. Hal ini jawaban adanya perubahan energi kinetik menjadi bentuk kalor dan atau suara pada ketika tumbukan. Jenis tumbukan ini disebut tumbukan tidak lenting sebagian. Bila sesudah tumbukan kedua benda bergabung, disebut tumbukan tidak lenting sempurna. Ada juga tumbukan dengan energi kinetik total tetap. Tumbukan jenis ini disebut tumbukan lenting (sempurna). Makara secara garis besar jenis- jenis tumbukan sanggup diklasifikasikan ke dalam:
1. Tumbukan lenting (sempurna)
Pada tumbukan lenting tepat berlaku:
a. Hukum kekekalan momentum
b. Hukum kekekalan Energi Kinetik
Bila kita uraikan dari kedua syarat
a. Hukum kekekalan momentum
m1 v1 + m2 v2 = m1 v'1+ m2 v'2
m1 v1 –m1 v'1 = m2 v'2 – m2 v2
m1 ( v1 – v'1 ) = m2 (v'2 – v2 )
( 1.1 )
a Hukum kekekalan energi kinetik
1/2 m1v12 + 1/2 m2v22 = 1/2 m1 v'12 + 1/2 m2 v'22
m1 v12 - m1 v'12 = m2v'22 – m2 v22
m1( v12 - v'12 ) = m2 (v'22 - v22 )
m1(v1 + v'1) (v 1 – v'1) = m2 (v'2 + v2) (v'2 – v2)
( 1.2 )
Bila persamaan (1.1) dibagi dengan persamaan (1.2) diperoleh :
(v1 + v'1) = (v'2 + v2)
atau
(v2 – v1) = - (v'2 - v'1)
( 1.3 )
Dengan kata lain kecepatan relatif kedua benda sebelum tumbukan sama dengan harga minus dari kecepatan relatif kedua benda sesudah tumbukan.
Untuk keperluan lebih lanjut didefenisikan :
( 1.4 )
berlaku jikalau v1 , v'1 , v2 , v'2 pada satu arah sumbu yang sama. Harga v yang dimasukkan disini harus memperhatikan arah (tanda + atau -), e ini yang lalu disebut koefisien restitusi, untuk tumbukan lenting (sempurna) e = 1, untuk tumbukan tidak lenting sebgian 0 < e < 1, untuk tumbukan tidak lenting tepat e = 0.
2. Tumbukan tidak lenting sebagian
Pada jenis tumbukan ini berlaku Hukum kekekalan momentum dan tidak berlaku aturan kekekalan energi kinetik sebab terjadi perubahan Ek. koefisien restitusi e yaitu pecahan.
Hukum kekekalan momentum
m1 v1 + m2 v2 = m1 v'1+ m2 v'2
dan 0 < e < 1
Tidak berlaku aturan kekekalan energi, berarti ada energi kinetik yang hilang selama proses tumbukan sebesar ∆Ek.
∆Ek = (1/2 m1v12 + 1/2 m2v22 ) - (1/2 m1 v'12 + 1/2 m2 v'22)
( 1.5 )
3. Tumbukan tidak lenting sempurna
Pada jenis tumbukan ini berlaku Hukum kekekalan momentum dan tidak berlaku aturan kekekalan energi kinetik sebab terjadi perubahan Ek. koefisien restitusi e = 0.
0 = -(v'2 – v'1)
v'1 = v'2
( 1.6 )
kecepatan selesai kedua benda sama dan searah. Berarti kedua benda bergabung dan bergerak bersama-sama.
Besar energi kinetik yang hilang ∆Ek
∆Ek = (1/2 m1v12 + 1/2 m2v22 ) - (1/2 m1 v'12 + 1/2 m2 v'22)
( 1.7 )
dimana : v'1 = v'2
Contoh Soal:
1. Dua buah benda A dan B masing-masing bermassa 2 kg dan 4 kg bergerak saling mendekat dengan kecepatan berturut-turut 4 m/s dan 3 m/s. Setelah tumbukan, massa A bergerak berlawanan dengan arah semula dengan kecepatan 5 m/s. tentukan:
a. Kecepatan benda B sesudah tumbukan
b. Koefisien restitusinya
c. Energi kinetik sistem yang hilang selama tumbukan
Diketahui :
mA = 2 kg
mB = 4 kg
vA = 4 m/s
vB = -3 m/s
v'A = - 5 m/s
Ditanya:
a. v'B = .... ?
b. e = .... ?
c. ∆Ek = .... ?
Jawab:
Ambil arah kekanan sebagai arah positif
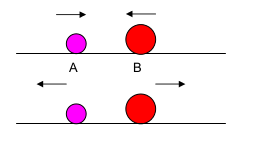
a. Kecepatan benda B sesudah tumbukan:
mA vA + m B vB = mA v'A + mB v'B
2 kg . 4 m/s + 4 kg . (-3 m/s) = 2 kg (-5 m/s) + 4 kg v'B
4 kg v'B = 6 kg m/s
v'B = 1.5 m/s
Tanda positif menyatakan bahwa arah kecepatan benda B sesudah tumbukan ke kanan
b. Koefisien restitusi e
Ambil arah ke kanan sebagai arah positif
pada rumus ini, harus diperhatikan tanda (+) atau (-) pada kecepatan.
e = 0,93
perhatikan tanda sistem plus dan minusnya
c. Energi kinetik yang hilang selama tumbukan
∆Ek = (1/2 m1v12 + 1/2 m2v22 ) - (1/2 m1 v'12 + 1/2 m2 v'22)
∆Ek = (1/2 2 . 42 + 1/2 4 . 32 ) - (1/2 2 . 52 + 1/2 4. 1,52)
∆Ek = 34 – 29,5 = 4,5 joule
Belum ada Komentar untuk "Jenis-Jenis Tumbukan (Lenting Sempurna, Sebagian Dan Tidak Sama Sekali) Beserta Pola Soal"
Posting Komentar