Pengertian Percepatan Rata-Rata Dan Sesaat Beserta Rujukan Soal
Percepatan yaitu perubahan kecepatan per satuan waktu. Seperti kecepatan, percepatan juga merupakan besaran vektor.
1. Percepatan Rata-Rata
Percepatan rata-rata yaitu perubahan kecepatan dibagi dengan waktu yang dibutuhkan untuk perubahan tersebut. Perhatikan Gambar berikut!
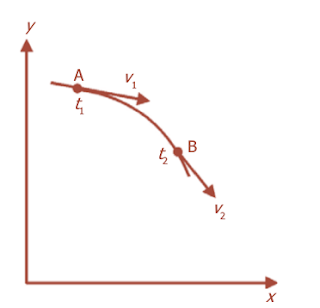
Percepatan rata-rata suatu benda yang bergerak dari A ke B.
Pada ketika t1 , sebuah partikel berada di A dengan kecepatan sesaat v1 dan pada ketika t2 partikel berada di B dengan kecepatan sesaat v2 , percepatan rata-rata selama bergerak dari A ke B adalah:
(1)
dengan:
a = percepatan rata-rata (m/s2 )
Δv = perubahan kecepatan (m/s)
Δt = selang waktu (s)
Persamaan (1) jikalau diciptakan dalam vektor satuan, maka:
a = axi + ayj
(2)
dengan:
2. Percepatan Sesaat
Percepatan sesaat didefinisikan sebagai limit kecepatan rata-rata untuk interval waktu mendekati nol.
(3)
jka v = vx i + vy j ,mka :
a = axi + ayj
(4)
dengan :
a = vektor percepatan
Dari persamaan (4) sanggup dikatakan bahwa percepatan merupakan turunan dari fungsi kecepatan terhadap waktu. Percepatan juga merupakan turunan kedua fungsi posisi terhadap waktu.

Percepatan sesaat merupakan kemiringan grafik kecepatan terhadap waktu.
Kerena:
maka persamaan (4) sanggup dituliskan:
(5)
Sehingga percepatan sesaat menjadi:
(6)
Contoh Soal:
1. Sebuah partikel bergerak dengan persamaan kecepatan v = (3+4t)i + (3t2)j, v dalam m/s dan t dalam s, tentukan:
a. besar percepatan rata-rata dari = 0 hingga t = 2 s,
b. besar percepatan ketika t = 1 s dan t = 2 s!
Penyelesaian:
a. Percepatan rata-rata
t = 0s → v0 = (3 + (4)(0))i + 3(0)2 j = 3i
t = 2s → v = v2 = (3 + (4)(2))i + 3(2)2 j = 11 i + 12
Besarnya percepatan rata-rata:
b. Percepatan sesaat
a = 4i + (6t)j
Besarnya percepatan:
2. Suatu partikel bergerak lurus dengan persamaan gerak r = t3 – 2t2 + 10t + 3, r dalam meter dan t dalam sekon. Tentukan:
a. kecepatan ketika t = 2 sekon,
b. percepatan ketika t = 2 sekon,
c. percepatan rata-rata untuk t = 1 s dan t = 3 s!
Penyelesaian:
a. v = dr/dt = 3t2 – 4t + 10
t = 2s → v = 3(2)2 – 4(2) + 10 = 12 – 8 + 10 = 14 m.s
b. a = dv/dt = 6t – 4
t = 2s → a = (6)(2) – 4 = 8 m/s2
c. t = 1s → v1 = (3)(1)2 – (4)(1) + 10 = 9 m/s
t = 3s → v1 = (3)(3)2 – (4)(3) + 10 = 25 m/s
3. Menentukan Kecepatan dari fungsi Percepatan
Berdasarkan persamaan (3), maka:
Fungsi kecepatan sanggup ditentukan dengan mengintegralkan fungsi percepatan tersebut.
Apabila ketika t0 kecepatannya v0 dan pada ketika t kecepatannya v, maka batas-batas integralnya adalah:
(7)
dengan:
v0 = kecepatan awal, pada ketika t0 (m/s)
v = kecepatan pada ketika t (m/s)
a = percepatan yang merupakan fungsi waktu (m/s2)
Apabila vektor kecepatan dan percepatan dinyatakan dalam komponen-komponennya, maka:
(8)
Contoh Soal:
1. Partikel bergerak lurus dengan persamaan percepatan a = 3i + (4t)j, a dalam m/s2 dan t dalam s. Jika kecepatan awal partikel v0 = 2i + 3j, tentukan persamaan kecepatan partikel tersebut!
Penyelesaian:
Diketahui:
a = 3i + (4t)j
v0 = 2i + 3j
Ditanya:
v = ... ?
Jawab:
v = 2i + 3j + (3t)i + (2t2)j = (2 + 3t)i + (3 + 2t2 )j
Jadi, persamaan kecepatannya v = (2 + 3t)i + (3 + 2t 2 )j
2. Sebuah benda bergerak lurus dengan persamaan percepatan a = 2 + 4t, a dalam m/s2 dan t dalam sekon. Jika kecepatan awal dan posisi awal benda masing-masing 2 m/s dan 5 m, tentukan:
a. persamaaan kecepatan,
b. posisi benda ketika t = 3 s!
Penyelesaian:
Diketahui:
a = 2 + 4t
v0 = 2 m/s
r0 = 5 m
Ditanya:
a. v = ... ?
b. r = ... ?
Jawab:
a.
Jadi, persamaan kecepatannya yaitu v = (2 + 2t + 2t2) m/s
b.
atau
Pada ketika t = 3 sekon, maka:
Belum ada Komentar untuk "Pengertian Percepatan Rata-Rata Dan Sesaat Beserta Rujukan Soal"
Posting Komentar