Penjelasan Mengenai Aturan Hooke Beserta Pola Soal
Hubungan antara gaya F yang meregangkan pegas dengan pertambahan anjang pegas x pada kawasan elastisitas pertama kali dikemukakan oleh Robert Hooke (1635 - 1703), yang lalu dikenal dengan Hukum Hooke. Pada kawasan lentur linier, besarnya gaya F sebanding dengan pertambahan panjang x.
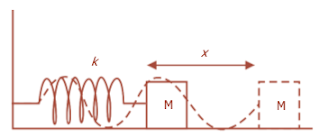
Gaya yang bekerja pada pegas sebanding dengan pertambahan panjang pegas.
Secara matematis dinyatakan:
F = k . x
(1)
dengan:
F = gaya yang dikerjakan pada pegas (N)
x = pertambahan panjang (m)
k = konstanta pegas (N/m)
Pada ketika ditarik, pegas mengadakan gaya yang besarnya sama dengan gaya tarikan tetapi arahnya berlawanan (Faksi = -Freaksi ). Jika gaya ini disebut gaya pegas FP maka gaya ini pun sebanding dengan pertambahan panjang pegas.
Fp = -F
Fp = - k.x
(2)
dengan:
Fp = gaya pegas (N)
Berdasarkan persamaan (1) dan (2), Hukum Hooke sanggup dinyatakan:
"Pada kawasan elastisitas benda, besarnya pertambahan panjang sebanding dengan gaya yang bekerja pada benda"
Sifat pegas ibarat ini banyak dipakai dalam kehidupan sehari-hari, contohnya pada neraca pegas dan pada kendaraan bermotor (pegas sebagai peredam kejut). Dua buah pegas atau lebih yang dirangkaikan sanggup diganti dengan sebuah pegas pengganti. Tetapan pegas pengganti seri dinyatakan oleh persamaan:
Adapun tetapan pegas pengganti paralel (kp) dinyatakan oleh persamaan: kp = k1 + k2 + k3 + ... kn.
Contoh Soal
Sebuah pegas yang panjangnya 15 cm digantungkan vertikal. Jika diberikan gaya 0,5 N, panjang pegas menjadi 25 cm. Berapakah panjang pegas jikalau diregangkan oleh gaya 0,6 N?
Penyelesaian:
Diketahui:
L0 = 15 cm
L1 = 25 cm
F1 = 0,5 N
F2 = 0,6 N
Ditanya:
x = ....? (F = 0,6 N)
Jawab:
x = L1 – L0 = (25 – 15) cm = 10 cm = 0,1 m
F1 = k.x
Untuk F2 = 0,6 N, maka:
F2 = k.x
Jadi, panjang pegas = L0 + x = (15 + 12) cm = 27 cm
Belum ada Komentar untuk "Penjelasan Mengenai Aturan Hooke Beserta Pola Soal"
Posting Komentar