Penjelasan Mengenai Aturan Pergeseran Wien
Untuk sebuah benda hitam, berlaku suatu relasi antara panjang gelombang dengan suhu mutlak yang dinyatakan:
λm .T = C
dengan λm merupakan panjang gelombang yang sesuai dengan radiasi energi maksimum, T yakni temperatur termodinamik benda, dan C yakni tetapan pergeseran Wien (2,898 × 10-3 mK). Hubungan tersebut disebut Hukum pergeseran Wien, yang dinyatakan oleh Wilhelm Wien (1864 – 1928)

Grafik relasi pergeseran Wien.
Gambar diatas memperlihatkan grafik relasi antara intensitas radiasi dan panjang gelombang radiasi benda hitam ideal pada tiga temperatur yang berbeda. Grafik ini dikenal sebagai grafik distribusi spektrum. Intensitas merupakan daya yang dipancarkan per satuan panjang gelombang. Ini merupakan fungsi panjang gelombang I maupun temperatur T, dan disebut distribusi spektrum. Dari grafik terlihat bahwa puncak kurva penyebaran energi spektrum bergeser ke arah ujung spektrum panjang gelombang pendek dengan semakin tingginya temperatur.
Fungsi distribusi spektrum P( λ ,T ) sanggup dihitung dari termodinamika klasik secara langsung, dan jadinya sanggup dibandingkan dengan Gambar diatas. Hasil perhitungan klasik ini dikenal sebagai Hukum Rayleigh- Jeans yang dinyatakan:
P ( λ ,T ) = 8 π kT λ-4
dengan k merupakan konstanta Boltzmann.
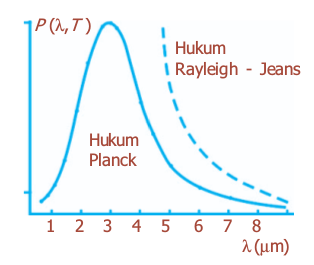
Distribusi spektrum radiasi benda hitam terhadap panjang gelombang pada T = 1.600 K.
Hasil ini sesuai dengan hasil yang diperoleh secara percobaan untuk panjang gelombang yang panjang, tetapi tidak sama pada panjang gelombang pendek. Begitu λ mendekati nol, fungsi P ( λ , T ) yang ditentukan secara percobaan juga mendekati nol, tetapi fungsi yang dihitung mendekati tak terhingga alasannya yakni sebanding dengan λ− 4. Dengan demikian, yang tak terhingga yang terkonsentrasi dalam panjang gelombang yang sangat pendek. Hasil ini dikenal sebagai katastrof ultraviolet.
Belum ada Komentar untuk "Penjelasan Mengenai Aturan Pergeseran Wien"
Posting Komentar