Soal Dan Pembahasan Gerak Lurus - Fisika Dasar
Jawablah Soal perihal Gerak Lurus berikut ini dengan baik dan benar!
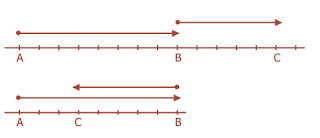
1. Rena berjalan ke Timur sejauh 80 m, lalu berbalik arah ke Barat menempuh jarak 50 m. Perjalanan tersebut memerlukan waktu 50 s. Berapakah kelajuan rata-rata dan kecepatan rata-rata Rena dalam perjalanannya?
Penyelesaian:
Jarak total = AB + BC = 80 m + 50 m = 130 m
Perpindahan = AB – BC = AB – BC = 80 m – 50 m = 30 m
Kelajuan rata-rata = 
Kecepatan rata-rata =
2. Seekor kucing bergerak pada lintasan garis lurus dan dinyatakan dalam persamaan x = 2t2 + 5t – 3 (x dalam meter dan t dalam sekon). Berapakah kecepatan sesaat kucing pada t = 2 s?
Penyelesaian: Kecepatan sesaat ditentukan dengan mengambil Δ t sekecil mungkin pada t = 2 s,
maka x1 = x pada t = 2 s, x1 = 2 (2)2 + 5 (2) – 3 = 15 m
Jika Δ t = 0,1 s, maka t 2 = 2,1 s
x 2 = 2 (2,1) 2 + 5 (2,1) – 3 = 16,32 m
Kecepatan rata-rata = 
Jika t 1 = 0,01 s, maka t 2 = 2,01 s
x 2 = 2 (2,01) 2 + 5 (2,01) – 3 = 15,1302 m
Kecepatan rata-rata = 
Jika Δ t = 0,001 s, maka t 2 = 2,001 s
x 2 = 2 (2,001) 2 + 5 (2,001) – 3 = 15,013002 m
Kecepatan rata-rata = 
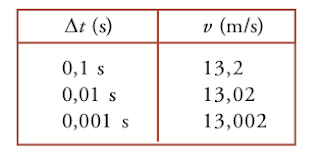
Dari tabel di atas, semakin kecil Δ t yang diambil, maka kecepatan rata-rata mendekati 13 m/s. Jadi, sanggup disimpulkan bahwa kecepatan sesaat kucing pada
t = 2 s yakni 13 m/s.
3. Kecepatan gerak sebuah kendaraan beroda empat berubah dari 10 m/s menjadi 16 m/s dalam selang waktu 3 sekon. Berapakah percepatan rata-rata kendaraan beroda empat dalam selang waktu tersebut?
Penyelesaian:
Diketahui:
v 1 = 10 m/s
v 2 = 16 m/s
Δ t = 3 s
Ditanya:  = ... ?
= ... ?
Jawab:
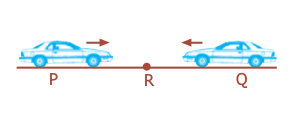
4. Sebuah kendaraan beroda empat bergerak dengan kecepatan 72 km/jam. Pada jarak 18 km dari arah yang berlawanan, sebuah kendaraan beroda empat bergerak dengan kecepatan 90 km/jam. Kapan dan di manakah kedua kendaraan beroda empat tersebut akan berpapasan?
Penyelesaian:
Jarak kedua kendaraan beroda empat = PQ = 18 km = 18.000 m
Misal, titik R merupakan titik di mana kedua kendaraan beroda empat tersebut berpapasan, maka:
PQ = PR + QR
Dengan:
PR = jarak tempuh kendaraan beroda empat 1
QR = jarak tempuh kendaraan beroda empat 2
Maka:
PQ = v1 t + v2 t
18.000 = (20t + 25t)
18.000 = 45 t
45 t = 18.000
t = 400 s
PQ = v1 .t = (20 m/s)(400 s) = 8.000 m = 8 km
QR = v2 .t = (25 m/s)(400 s) = 10.000 m = 10 km
Jadi, kedua kendaraan beroda empat tersebut berpapasan sesudah 400 s bergerak, dan sesudah kendaraan beroda empat pertama menempuh jarak 8 km atau sesudah kendaraan beroda empat kedua menempuh jarak 10 km.
5. Sebuah kendaraan beroda empat mulai bergerak dari keadaan membisu dengan percepatan tetap 8 m/s 2. Berapakah kecepatan kendaraan beroda empat sesudah bergerak selama 6 sekon?
Penyelesaian:
Diketahui : v 0 = 0; a = 8 m/s 2 ; t = 6 s
Ditanya : vt = ... ?
Jawab :
vt = v 0 + at = 0 + (8 m/s 2 ) (6 s)
vt = 48 m/s
6. Doni melempar sebuah bola dari puncak gedung apartemen setinggi 37,6 m. Tepat pada ketika yang sama Yusuf yang tingginya 160 cm berjalan mendekati kaki gedung dengan kecepatan tetap 1,4 m/s. Berapa jarak Yusuf dari kaki gedung sempurna pada ketika bola jatuh, kalau bola yang dijatuhkan tersebut sempurna mengenai kepala Yusuf?
Penyelesaian:
Bola mengalami gerak jatuh bebas
v0 = 0
a = -g = -9,8 m/s2
Jarak tempuh bola = 37,6 m – 160 cm = 37,6 m – 1,6 m = 36 m. Jadi, y = -36.
Jika waktu tempuh Yusuf sama dengan waktu jatuh bola, maka bola tersebut akan mengenai kepala Yusuf. Yusuf mengalami gerak lurus beraturan dengan
v = 1,4 m/s, maka jarak Yusuf semula dari kaki gedung adalah:
7. Sebuah bola dilempar vertikal ke atas dengan kecepatan 60 m/s. Jika percepatan gravitasi g = 10 m/s2 , tentukan:
a. waktu yang dibutuhkan bola untuk mencapai ketinggian maksimum,
b. kecepatan bola ketika datang di tanah,
c. waktu yang dibutuhkan bola untuk kembali ke tanah!
Penyelesaian:
a. Bola mengalami gerak vertikal ke atas, maka a = -g = -10 m/s2 . Saat mencapai titik tertinggi, kecepatan bola yakni nol (v t = 0), maka:
v t = v 0 + at
0 = v 0 + at
b. Kecepatan pada ketika datang di tanah sama dengan kecepatan bola ketika di- lempar dari tanah, hanya saja tandanya menjadi negatif (-)
v A = -v 0 = -60 m/s (arah ke bawah)
c. Gerak bola pada ketika naik simetris dengan gerak bola ketika turun. Hal ini berarti waktu naik sama dengan waktu turun (t = 6 s), sehingga waktu yang dibutuhkan bola untuk kembali ke tanah adalah:
ttot = 2t = 2(6) s = 12 s
8. Sebuah bola dilemparkan ke atas dengan kecepatan awal 30 m/s. Jika percepatannya yakni 10 m/s2 ke bawah, berapa waktu yang dibutuhkan untuk mencapai titik tertingginya, dan berapakah jarak ke titik tertinggi itu?
Penyelesaian:
a. v = v0 + at
0 = 30 m/s + (-10 m/s2)t
b. Δ x = vrata-rata .t = (15 m/s)(3,0 s) = 45 m
Belum ada Komentar untuk "Soal Dan Pembahasan Gerak Lurus - Fisika Dasar"
Posting Komentar