Simpangan, Kecepatan, Dan Percepatan Pada Pegas

Penjelasan perihal Simpangan, Kecepatan, dan Percepatan pada Pegas - Simpangan pada gerak harmonik sederhana sanggup ditentukan melalui analogi sebuah titik yang bergerak melingkar beraturan. Kecepatan dan percepatan gerak harmonik sederhana merupakan turunan pertama dan kedua dari persamaan simpangan yang merupakan fungsi waktu.

1. Simpangan 

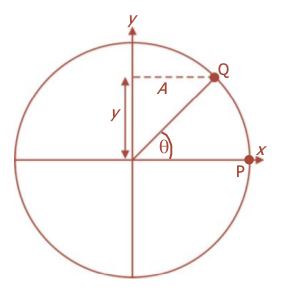
Gerak harmonik sederhana merupakan proyeksi titik P pada sumbu x.

Perhatikan gambar diatas. Sebuah partikel bergerak melingkar beraturan dengan jari-jari A dan kecepatan sudut ω. Pada dikala t = 0, partikel berada di titik P, sehabis t sekon berada di Q. Besarnya sudut yang ditempuh adalah:

(1)

Simpangan gerak harmonik sederhana sanggup dianggap proyeksi titik P pada salah satu sumbu utamanya (sumbu y). Jika simpangan itu dinyatakan dengan sumbu y, maka:

(2)

dengan:

y = simpangan gerak harmonik sederhana (m)

A = amplitudo (m)

T = periode (s)

ω = kecepatan sudut (rad/s)

t = waktu (s)

Fase gerak harmonik menyatakan keadaan gerak dalam hubungannya dengan simpangan dan arah getar. Jika suatu gerak harmonik kembali ke simpangan dan arah semula, maka gerak harmonik itu telah kembali ke fase semula.

Dari persamaan (2) diperoleh:

Atau y = A . sin 2πφ, dengan φ yakni fase yang dituliskan dengan:

(3)

Dua titik atau kedudukan dikatakan sefase jikalau beda fase sama dengan nol, dan dikatakan berlawanan fase jikalau beda setengah.

2. Kecepatan

Kecepatan gerak harmonik sederhana sanggup ditentukan dari turunan persamaan simpangan.

y = A. sin 2π (ω + θ₀)

v_y = ω . A . cos (ωt + θ₀)

(4)

Kecepatan gerak harmonik sederhana akan berharga maksimum jikalau fungsi cosinus bernilai maksimum, yaitu satu, sehingga:

v_maks = ω . A

(5)

Dari persamaan (4) kecepatan gerak harmonik sanggup dinyatakan sebagai berikut:

sin² (ωt + θ₀) + cos² (ωt + θ₀) = 1, maka

sehingga persamaan (4) menjadi:

karena:

y = A . sin( ωt + θ₀ ) , maka:

(6)

3. Percepatan

Percepatan pada gerak harmonik sederhana sanggup ditentukan dari turunan pertama persamaan kecepatan atau turunan kedua dari persamaan simpangan.

a_y = -ω² . A . sin (ωt + θ₀)

(7)

kerena A . sin (ωt + θ₀) = y, maka:

a_y = -ω² y

(8)

Percepatan akan bernilai maksimum jikalau fungsi sinus bernilai maksimum, yaitu satu, sehingga persamaan (5) menjadi:

a_maks = -ω² . A

(9)

Tanda negatif pada persamaan (7) dan (8) menunjukkan bahwa percepatan berlawanan dengan arah simpangannya.

4. Energi Gerak Harmonik Sederhana

Benda yang melaksanakan gerak harmonik sederhana mempunyai energi potensial dan energi kinetik. Jumlah energi potensial dan energi kinetik disebut energi mekanik. Besarnya energi potensial yakni energi yang dimiliki gerak harmonik sederhana alasannya yakni simpangannya. Secara matematis dituliskan:

E_p = 1/2 ky²

Karena: y = A.sin ωt , maka:

E_p = 1/2 k . A² . sin² ωt

(10)

Energi kinetik yakni energi yang dimiliki oleh benda yang melaksanakan gerak harmonik sederhana alasannya yakni kecepatannya. Secara matematis dituliskan:

Ek = 1/2 m.v²

Ek = 1/2 m.ω^{2 .}. A² . cos² ωt

kerena mω² = k, maka:

Ek = 1/2 k^{2 .}. A² . cos² ωt

(11)

Besarnya energi mekanik adalah:

Em = Ep + Ek

Em = 1/2 k . A² . sin² ωt + 1/2 k^{2 .}. A² . cos² ωt

Em = 1/2 k^{2 .}. A² . (sin² ωt + cos² ωt)

karena sin² ωt + cos² ωt = 1, maka:

Em = 1/2 k . A²

Besarnya energi mekanik dari suatu benda yang melaksanakan gerak harmonik sederhana yakni tetap, sehingga berlaku kekekalan energi mekanik yang sanggup dituliskan:

Em₁ = Em ₂

Ep₁ + Ek₁ = Ep₂ + Ek₂

(12)

Pada gerak harmonik sederhana, energi potensial akan minimum dikala simpangannya minimum (y = 0) dan maksimum dikala simpangannya maksimum (y = A). Sementara itu, energi kinetik akan minimum dikala simpangan maksimum (y = A) dan maksimum dikala simpangannya minimum (y = 0).

Energi potensial lentur pegas

Untuk meregangkan pegas sepanjang x diharapkan gaya sebesar F untuk menarik pegas tersebut. Energi potensial pegas yakni besarnya gaya pegas untuk meregangkan sepanjang x. Berdasarkan Hukum Hooke, sanggup diketahui grafik kekerabatan antara gaya F dengan pertambahan panjang x menyerupai yang terlihat pada gambar berikut:

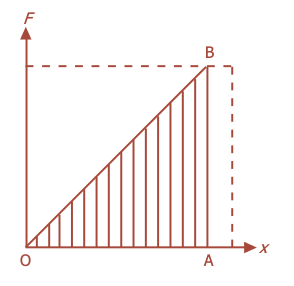
Grafik gaya terhadap pertambahan panjang.

Besarnya perjuangan merupakan luasan yang diarsir.

Ep = W = luas ΔOAB = 1/2 F . sx

alasannya yakni F = k . x, maka:

Ep = 1/2 (k . x)x

Ep = 1/2 k . x²

(13)

dengan:

Ep = energi potensial pegas ( J)

k = konstanta gaya pegas (N/m)

x = pertambahan panjang pegas (m)

Bagikan Artikel ini